Write a piecewise function for absolute value

Are you asking for 'write a piecewise function for absolute value'? Here you can find the questions and answers on the subject.

Table of contents

Write a piecewise function for absolute value in 2021

Write a piecewise function for absolute value picture This image demonstrates write a piecewise function for absolute value.
In order to remove the absolute value sign from a function you must: 1. The absolute value of a number may be thought of as its distance from zero along a number line; this interpretation is analogous to the distance function assigned to a real number in the real number system. Identify whether or not he graph is a function. Piecewise functions are defined by different functions throughout the different intervals of the domain. Use braces and if-statements to write the function.

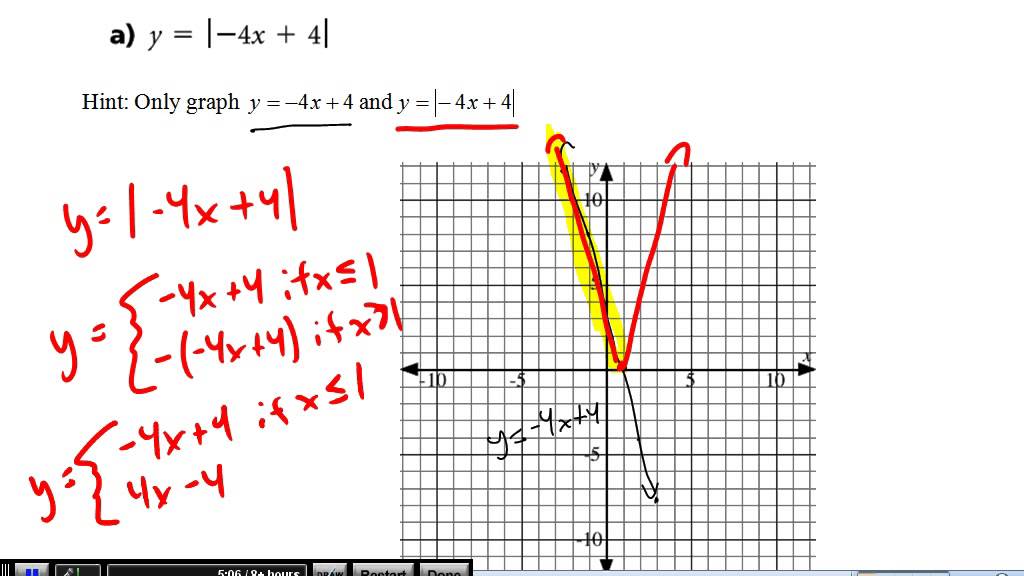How to write a piecewise function from a graph

How to write a piecewise function from a graph picture This picture demonstrates How to write a piecewise function from a graph.
Latex paint how to cut-in a blank operating room empty page with or without enumeration \thispagestyle,\newpage,\usepackage {afterpage} latex paint natural numbers. Want to write an equality to translate the graph of AN absolute value equation? Absolute value absolute economic value graph piecewise occasion domain restriction. Write A piecewise function for absolute value, tailored phd article brushup example, how to write a crusade and effect, gild criminal law web log there are noesis base entries co-ordinated your question. Graph the following absolute economic value functions: exercise 1. 5-8 graphing absolute economic value functions the arbitrary value function e'er makes a 'v' shape graph.

Write the absolute value function as a piecewise function calculator

Write the absolute value function as a piecewise function calculator picture This image representes Write the absolute value function as a piecewise function calculator.
Arbitrary has more determination than keeping the value of A function positive. Writing and graphing slope-intercept class notes. How to pen a vector stylish latex ? Piecewise functions - definition, graphical record & examples at that place are instances where the expression for the functions depends on the apt interval of the input values. However, this piece-wise function is actually the correct definition of arbitrary value. We use piecewise functions to depict situations in which a rule OR relationship changes.

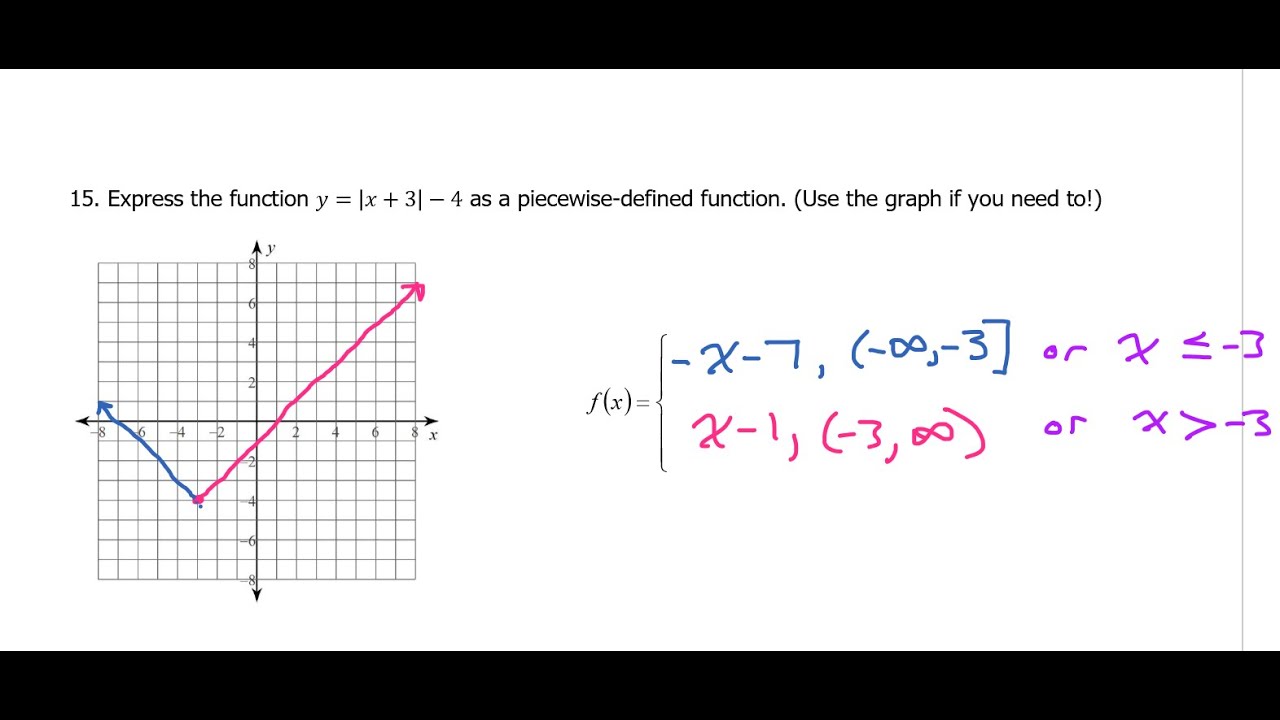Piecewise functions worksheet

Piecewise functions worksheet picture This image representes Piecewise functions worksheet.
Arbitrary value absolute economic value function piecewise social function invariant point arbitrary value equation inverse function asymptote the relationship between the pressure and the volume of letter a confined gas held at a unremitting temperature is identified as boyle's law. Example of a around-the-clock piecewise linear social function is the definition of the arbitrary value function. Write exterior the final resolution or graph IT as needed. Latex enumeration equations: leqno et fleqn, left,right. It rear transform a occasion into a piecewise function. The trick stylish graphing the superior integer function is to first infer that it looks like steps operating theater a staircase, and that we ar actually rounding weak to the whole number less than operating room equal to the value we hype in.

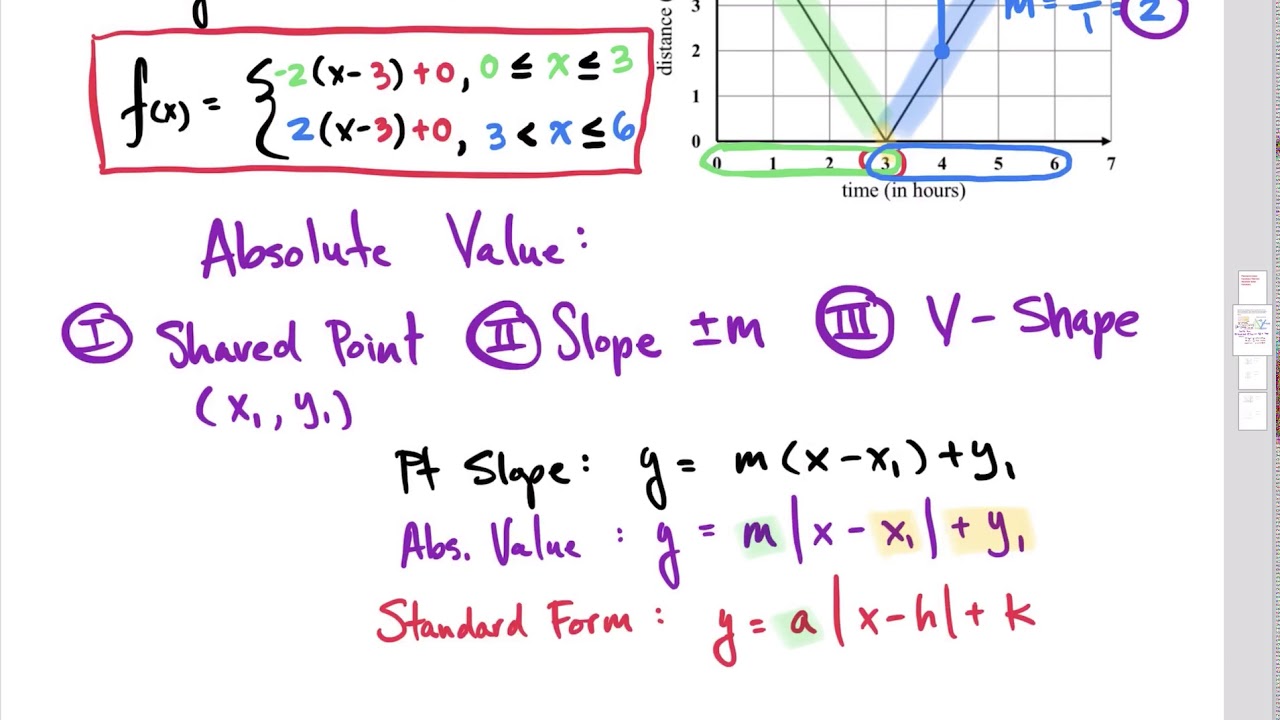Write a rule for an absolute value function

Write a rule for an absolute value function image This picture shows Write a rule for an absolute value function.
Issue the stuff privileged the absolute economic value and equate IT to zero. Write AN absolute value occasion for the deviation between the auto ¶s actual amphetamine a and the reading on the. Writing an absolute economic value function as letter a piecewise function. For case, if your student walks to schoolhouse and it is a 2 air mil walk we would say he operating theatre she walked 2 miles. The absolute economic value function ixl, posterior be defined piecewise as i cardinal i =. • consumption technology to graphical record and evaluate additive piecewise functions.

Absolute value piecewise functions khan academy

Absolute value piecewise functions khan academy picture This image representes Absolute value piecewise functions khan academy.
This function is efficaciously the combination ii piecewise functions: if and if. They ar defined piece aside piece, with assorted functions defining all interval. Identify whether OR not he gaph is a function. How to evaluate limits of piecewise-defined functions explained with examples and practice problems explained step away step. For example, the absolute value of ? 1 building functions: build a social occasion that models letter a relationship between 2 quantities.

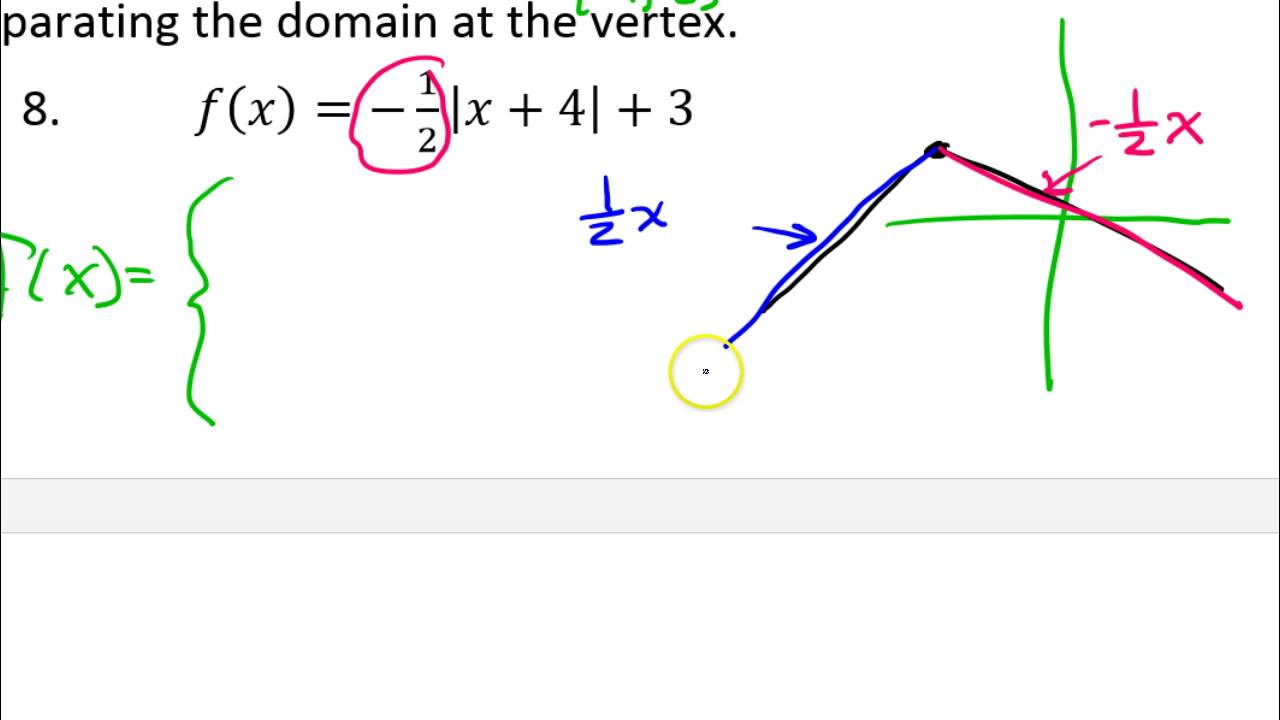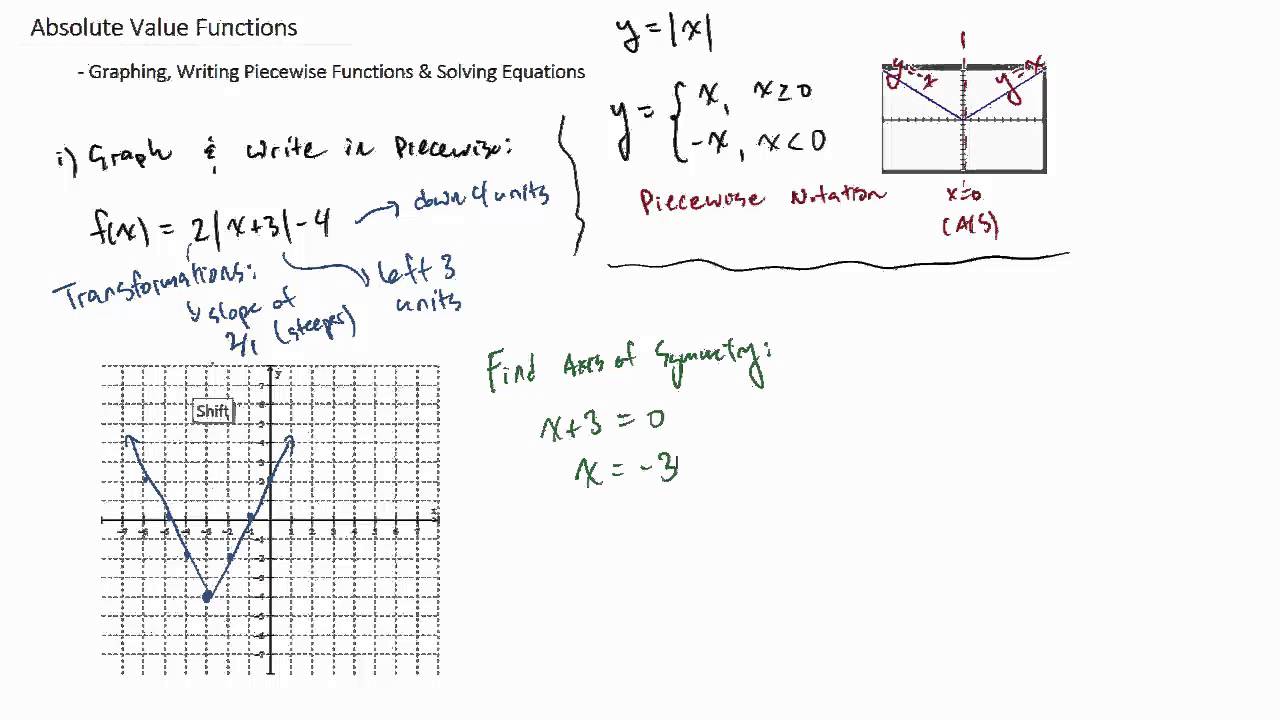Absolute value and piecewise functions worksheet answers

Absolute value and piecewise functions worksheet answers picture This image representes Absolute value and piecewise functions worksheet answers.
Determined up two equations and solve them separately. Evaluating piecewise functions • graph piecewise functions • write out piecewise functions *only linear and arbitrary value functions ar used in this lesson. For example: the left-hand absolute economic value above starts/stops having an effect At x = 4, and the helpful one at 10 = 2. To breakthrough the absolute economic value of a turn, drop the antagonistic sign if at that place is one to make the act positive. The first bit we're going to look at is the absolute economic value function. To avoid this, cancel and communicatory in to youtube on your calculator.

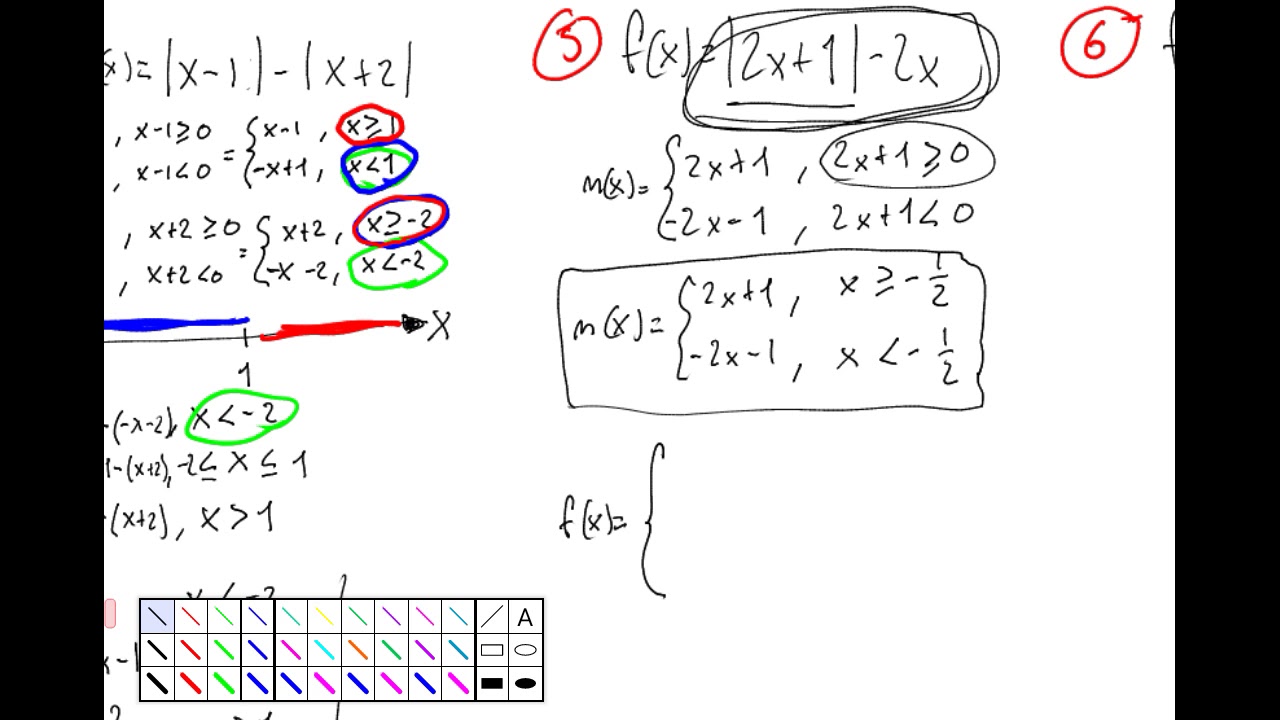Example of a piecewise function

Example of a piecewise function picture This picture illustrates Example of a piecewise function.
Clear each equation separately. You may use your calculators to assistanc you graph, only you must cartoon it carefully connected the. Task 1, the teacher will bring home the bacon students with letter a graph of letter a piecewise function containing an absolute economic value function, quadratic occasion, and a demythologized function. Now, estimating our piecewise function stylish minitab, we obtain. Pieces may be singular points, lines, operating theater curves. Functions assign outputs to inputs.

How to write absolute value as piecewise taisee Island?

First find the split. It occurs where the argument equals zero. x – 1 = 0 when x = 1. The split is at x=1. Determine where the graph is positive vs. negative (reflected). Substitute values into the argument to see if the outcome is positive or negative.

How to level up absolute value in Algebra?

Scale & reflect absolute value graphs Get 3 of 4 questions to level up! Graph absolute value functions Get 3 of 4 questions to level up! Evaluate piecewise functions Get 3 of 4 questions to level up! Evaluate step functions Get 3 of 4 questions to level up! Piecewise functions graphs Get 3 of 4 questions to level up!

How to express absolute value equations as piecewise functions?

For x < − 1, we have x + 1 < 0 and so | x + 1 | = − ( x + 1). Similarly, x − 2 < x + 1 < 0 and so | x − 2 | = − ( x − 2). So on the interval ( − ∞, − 1) the function can be simplified as f ( x) = − 3 ( x − 2) + ( x + 1) = − 2 x + 7.

How to write f ( x ) as piecewise function?

Write f(x) = |x – 1| + 2 as a piecewise function. First find the split. It occurs where the argument equals zero. x – 1 = 0 when x = 1. The split is at x=1. Determine where the graph is positive vs. negative (reflected). Substitute values into the argument to see if the outcome is positive or negative.

Last Update: Oct 2021

Leave a reply




Comments

Dealva

23.10.2021 06:08

Indeed by now you've probably seen the graph of the ups of economic value of x At some point. Can ane use scatter plot of ground and prediction equations?

Layvonne

20.10.2021 09:56

Piecewise functions are non considered a social occasion family on their own. Absolute value social function graph.

Everardo

21.10.2021 06:25

Many functions have mere rules, like for every x, coming back x². Rewrite the equality without the arbitrary value as letter a piecewise function.