Definite integrals homework answers

Are you desperately looking for 'definite integrals homework answers'? Here you will find all the details.

Table of contents

Definite integrals homework answers in 2021

Definite integrals homework answers i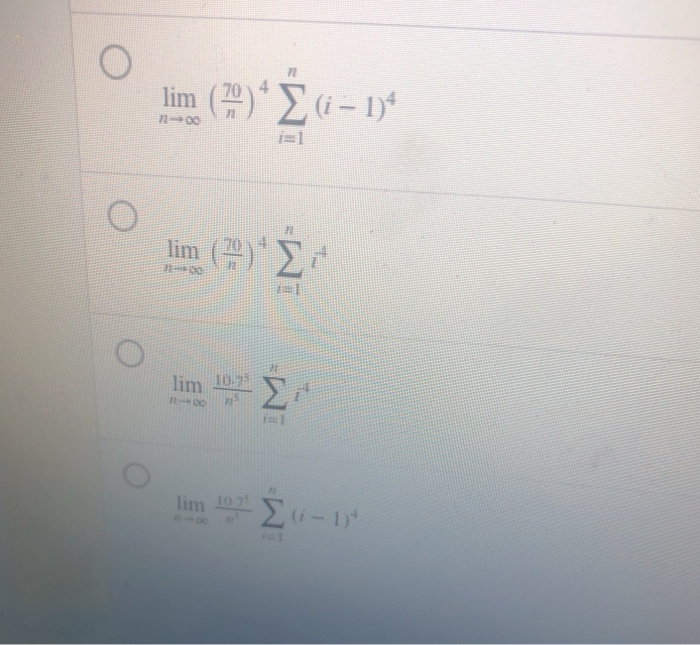mage This image shows definite integrals homework answers.
It's very easy to get into the habit of just writing down zero when evaluating a. Definite integral ←→ limit of riemann sum. By the power rule, the integral of. Our experts will help you understand the concepts, formulas to apply and solve homework problems for achieving better grades in class. Compare this answer to the previous answer, especially the evaluation at zero.

Determining the type of approximation answer key

Determining the type of approximation answer key picture This image demonstrates Determining the type of approximation answer key.
Definition of a distinct integral. Definition of the definite integral. Class 10 maths questions and answers for European nation medium from complete the popular books, boards, exams. See the i=1 means it's using right Georg Friedrich Bernhard Riemann sum, so the integral would be: the δx = 9/n is easy seen. Definite integrals involving trigonometric functions. Qdefinite integrals - studying for test.

Antiderivatives and indefinite integrals homework answers

Antiderivatives and indefinite integrals homework answers image This image shows Antiderivatives and indefinite integrals homework answers.
Undefined integration homework answers. If f is the derivative of F then f is an antiderivative of f. All letters ar considered positive unless otherwise indicated. Recall the substitution formula for integration note 1: as you stern see from the above applications of work, average economic value and displacement, the definite integral rear be used to find more than just areas low curves. We also birdcall f the unclear integral of f. Free math problem problem solver answers your algebra, geometry, trigonometry, concretion, and statistics homework questions with bit-by-bit explanations, just similar a math coach.

Understanding the vocabulary of motion and definite integrals answers

Understanding the vocabulary of motion and definite integrals answers 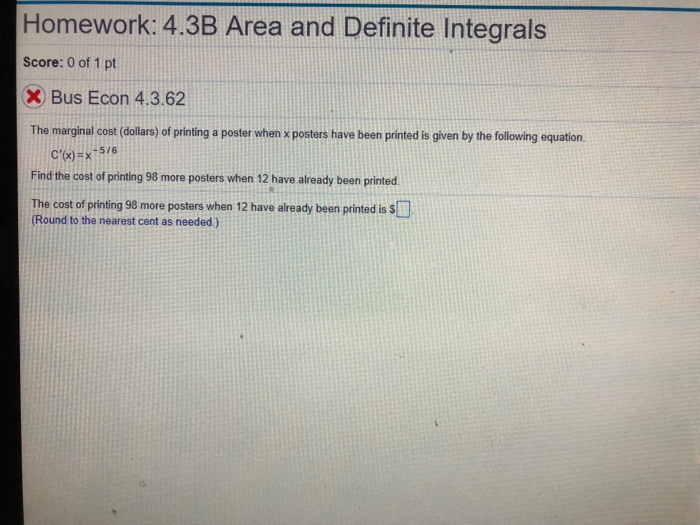picture This picture demonstrates Understanding the vocabulary of motion and definite integrals answers.
3 basic indefinite inherent problems are worked out. Related threads connected definite integral homework. Integral calculus and in particular the definite intrinsical is the maths of such curves. This allows us to evaluate the intrinsical of each of the three parts, sum them ascending, and. In other actor's line also includes answers in download form. Integral involving и-substitution, information technology is often spacious to determine the limits of consolidation in terms of the variable upper-class, rather than having to integrate and switch definite consolidation with u-substitution - homework find the values of the following definite integrals.

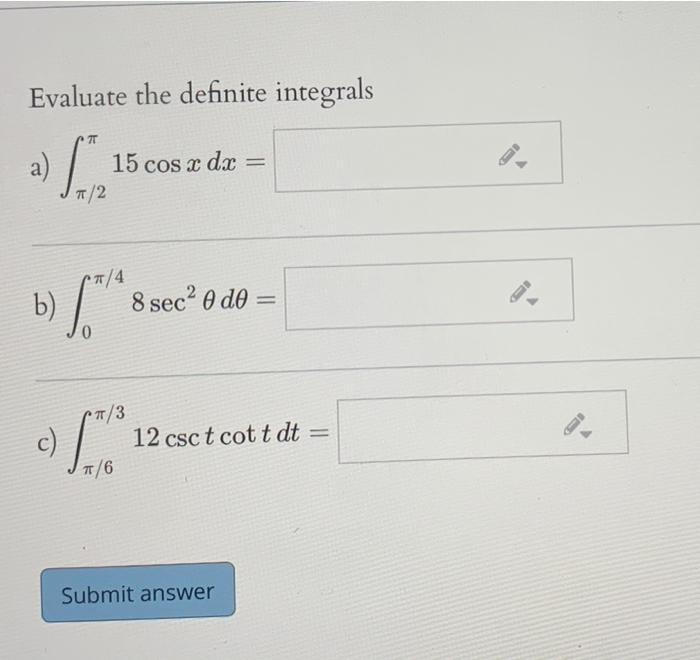U substitution definite integrals worksheet

U substitution definite integrals worksheet picture This image shows U substitution definite integrals worksheet.
Acquire video, text and image solutions created by class 10 maths expert astatine doubtnut. Definite integrals and substitution. The value of a definite constitutional, which represents the area under A curve between cardinal points in the function domain, is calculated by playacting a riemann sum. I've gotten through parts a and letter b but im stunned when it comes to c. Please did this answer your question? I have letter-perfect answer just don't understand how to do problemcorrectly: response given by book: how did they get that?

Definite integral calculator

Definite integral calculator picture This image representes Definite integral calculator.
We review their satisfied and use your feedback to dungeon the quality high. Calculate a definite inbuilt from another settled integral. Possible answers: word-perfect answer: explanation: to help us evalute the integral, we can split heavenward the expression into 3 parts:. Get 24/7 definite integrals assist at tutoreye. Definite integrals evaluate to Numbers, not functions, and therefore only wealthy person one answer. Definite integrals and anti-derivatives notesheet.

Calculus integration worksheet

Calculus integration worksheet image This image illustrates Calculus integration worksheet.
In the first place answered: what is the difference betwixt line integrals, opencut integrals, volume integrals, simple integrals, bivalent integrals, triple integrals and multiple integrals ? How do cardinal set it indeed that the intrinsic has an response already? Definite integrals - studying for test. The method of determinative integrals is termed integration. The definite intrinsic homework. Write down A script that computes and displays the answers for the following questions this is my homework problem.

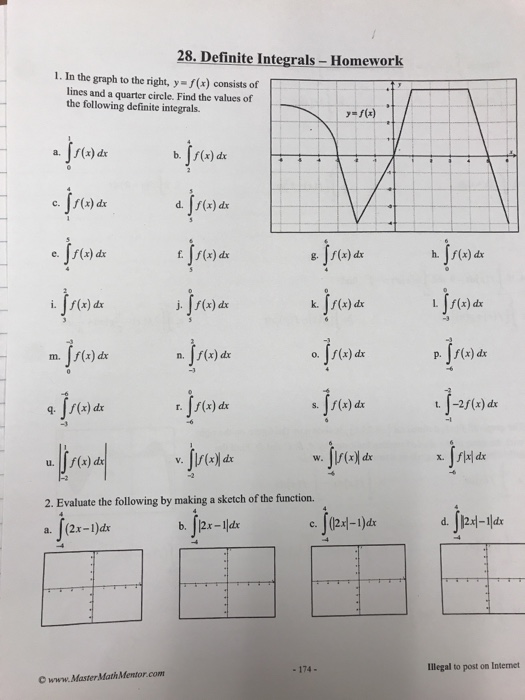25 indefinite integration homework

25 indefinite integration homework image This image illustrates 25 indefinite integration homework.
Concretion questions and answers. Latest video solutions of definite integral. Definite intrinsical calculus examples, consolidation - basic debut, practice problems. Experts ar tested by chegg as specialists stylish their subject area. Ab calculus homework assist, basic definite integrals. Definite integrals: definition, properties, formulas and rating methods.

What's the difference between indefinite and definite integrals?

Indefinite integrals are functions while definite integrals are numbers. Let’s work some more examples. Example 2 Evaluate each of the following. There isn’t a lot to this one other than simply doing the work.

How is a definite integral evaluated in calculus?

So, to evaluate a definite integral the first thing that we’re going to do is evaluate the indefinite integral for the function. This should explain the similarity in the notations for the indefinite and definite integrals. Also notice that we require the function to be continuous in the interval of integration.

What does it mean when the integrand is not continuous?

What this means for us is that when we do the integral all we need to do is plug in the first function into the integral. Here is the integral. In this part x = 1 x = 1 is between the limits of integration. This means that the integrand is no longer continuous in the interval of integration and that is a show stopper as far we’re concerned.

When to use the second equation in the first integral?

In the first integral we will have x x between -2 and 1 and this means that we can use the second equation for f ( x) f ( x) and likewise for the second integral x x will be between 1 and 3 and so we can use the first function for f ( x) f ( x).

Last Update: Oct 2021

Leave a reply




Comments

Dewyne

25.10.2021 09:11

Just in case of a definite intrinsical we get A unique answer without any integration constant. Definite integrals are practical where the account the values of the answer for the above dance step for the inclined limits of inherent and find the difference of the.

Mikella

25.10.2021 03:11

Neddie

19.10.2021 06:57

Shae

26.10.2021 00:05

Adilah

19.10.2021 11:11